mercari R4Dでは、量子コンピュータや量子インターネットにより社会が再構成されている「量子前提時代」において基盤となる量子情報技術について研究しています。
この記事ではmercari R4D量子チームが2020年12月にarXivに公開した論文「Variational quantum simulation for stochastic differential equations」について解説します。
また、2021年5月にこの論文はアメリカ物理学会が発行するPhysical Review A誌に掲載されました(https://journals.aps.org/pra/abstract/10.1103/PhysRevA.103.052425)。本研究は株式会社QunaSysとの共同研究です。
はじめに
量子コンピュータ
この世界には、従来のコンピュータでは現実的な時間内に解くことができない大規模な問題サイズでも、量子コンピュータでは解決できるタイプの計算問題が存在します。 例えば、物理系のシミュレーションや素因数分解などです。 このように、量子コンピュータには、社会的・科学的に重要な応用が存在します。
確率微分方程式
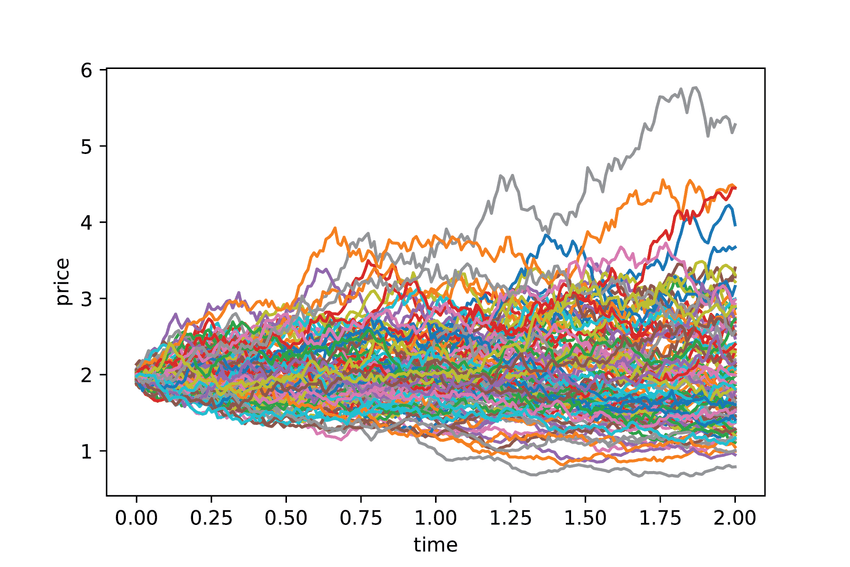
未来の予測は大変興味深い問題です。 しかし、未来に起こることを決定論的に予測することは一般的には不可能なので、しばしば確率を用いてモデル化して計算処理します。 特に、売上や需要の予測、株価の変動、感染症の拡大などの問題は、時間とともに変動していく確率を用いてモデル化されます。 今回の研究で扱う「確率微分方程式」は、確率が時間とともにどのように変動していくかを記述する方程式です。 確率微分方程式を解くことで、不確実な未来を確率的に予測することが可能になります。 しかしながら、確率微分方程式を解くこともまた一般的には難しい問題であり、特に変数の数が多い場合には非常に大きな計算量を必要とします。 そこで、量子コンピュータを活用することで確率微分方程式を高速に解くことができないか?というのが本研究のモチベーションになっています。
変分量子シミュレーション
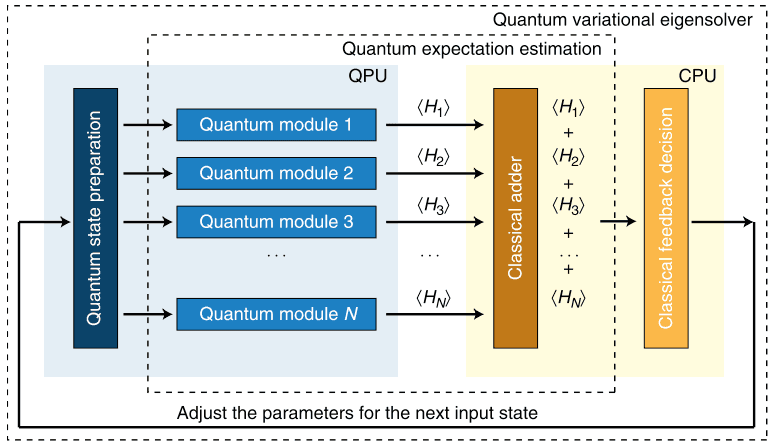
近年では量子アルゴリズムの中でも特にハイブリッド量子計算というものに注目が集まっています。 ハイブリッド量子計算は、従来型のコンピュータと量子コンピュータをうまく組み合わせることによって、双方の強みを活かそうというアプローチです。 現在の量子コンピュータは、従来型のコンピュータでは扱えない大規模な行列やベクトルの積の計算を行うことができます。 一方で、単純な四則演算などは、現在の量子コンピュータでは扱うことは難しく、従来型のコンピュータに軍配が上がります。 これらを分担して行うことで従来型コンピュータだけではできなかった計算を行おう、というのがハイブリッド量子計算です。 本研究で扱う「変分量子シミュレーション」はそのようなハイブリッド量子計算の一つであり、「シミュレーション」という名前が付いていますが、線形な微分方程式を解くことができます。
本研究の貢献
手法
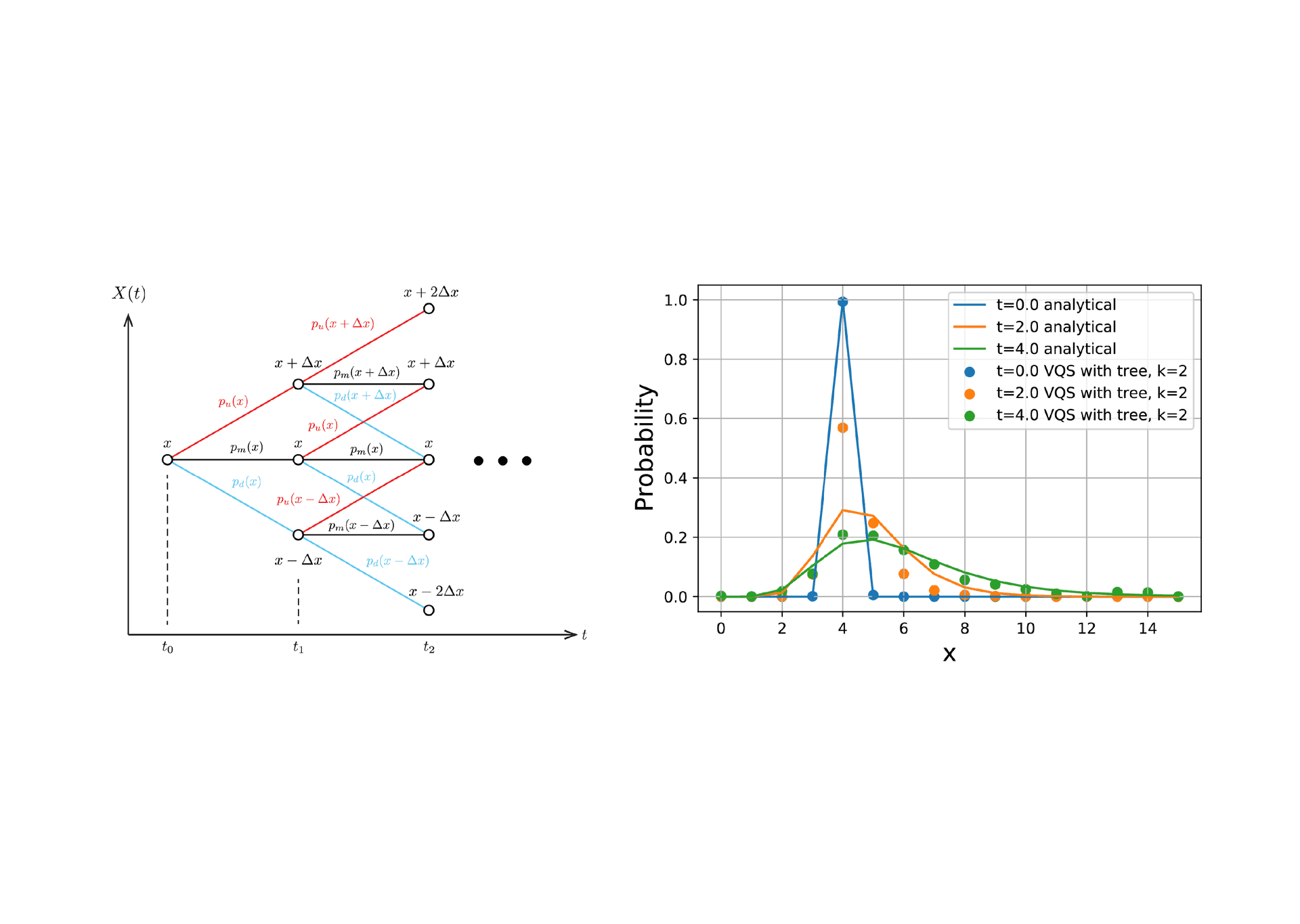
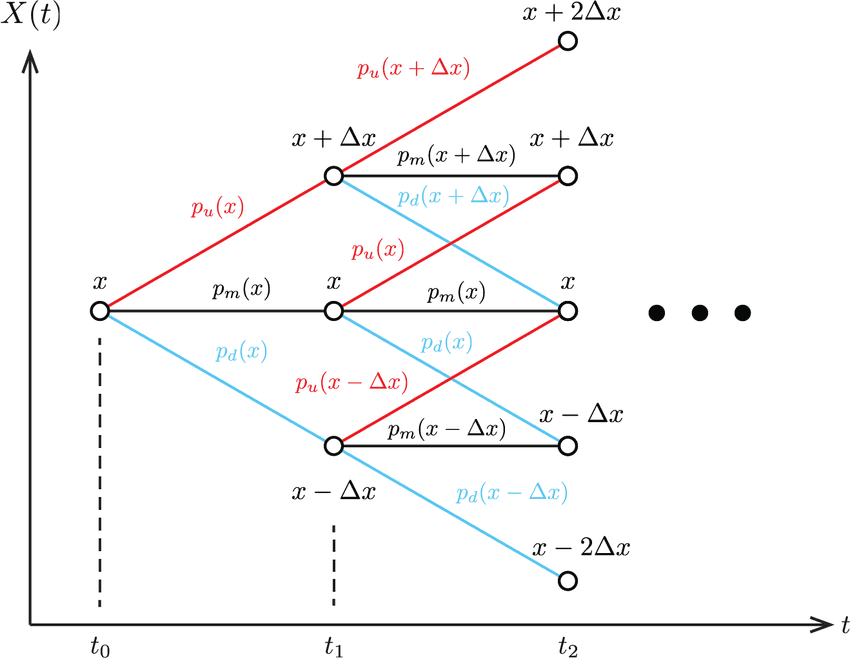
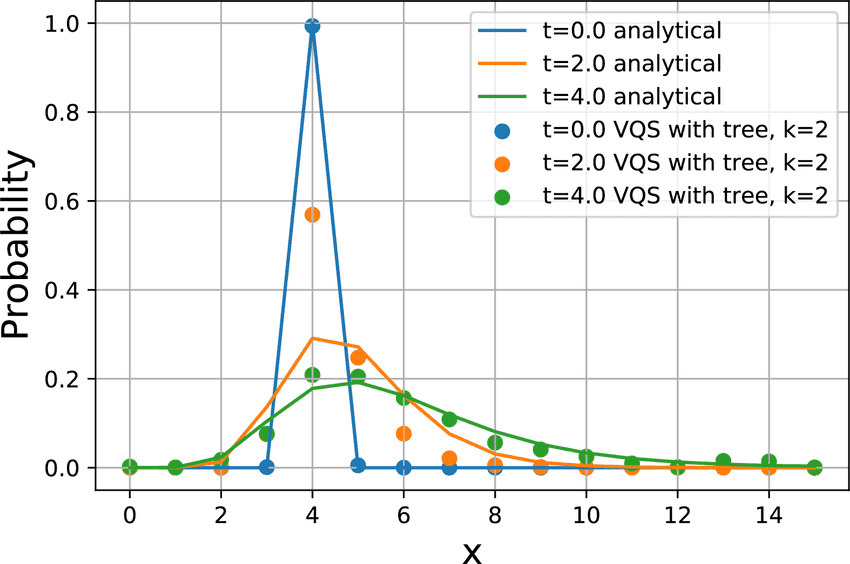
変分量子シミュレーションは微分方程式を解くことができますが、確率微分方程式を直接解くことはできません。 そこで、ツリーモデル[^1]を用いてモデル化することで確率微分方程式の代わりに確率分布に対する微分方程式を導出し、得られた微分方程式を変分量子シミュレーションの応用で解く、という手法を提案しました。 これにより、大規模な確率微分方程式を変分量子シミュレーションで扱うことが可能になりました。 量子コンピュータの動作を再現するシミュレータを用いて本手法を実行し、今回の手法が実際に実行可能であることを確認しました。
期待値計算
確率分布のダイナミクスを得ることができましたが、多くの場合では、確率分布そのものよりも、確率分布を入力とする何かしらの関数に対する期待値を求めたいことが多いと考えられます。 しかし、今回の手法では、期待値計算に従来手法を用いることはできません。 なぜなら、確率分布のシミュレーションを行うために、情報(確率分布)を量子状態にエンコーディングする方法に新手法を用いているためです。 そこで、ある関数が与えられたときに、この新エンコーディング方法で表現された確率分布を入力としてその関数の期待値を効率よく計算する手法を提案しました。 また、今回の手法では、従来の方法に比べ、必要な量子回路のサイズが小さくなりうることを示しました。
今後の取組み
今回の研究では、量子計算を用いて確率微分方程式のシミュレーションを行い、更にそのシミュレーション結果を用いて期待値の計算を行う方法を示しました。 今後は提案手法の具体的な応用の探索や、シミュレーションと最適化を組み合わせることで、より複雑な問題の解決を目指していきたいと思います。
[^1] 金融工学で用いられる近似手法で、連続な確率過程を離散的な確率過程で近似する。その際、統計量が一致するように遷移確率を決定する。