At mercari R4D, we are researching quantum information technology, the basis of the “quantum-based era” in which society is reconstructed by quantum computers and the quantum Internet.
This article describes a paper “Variational quantum simulation for stochastic differential equations” published on arXiv in December 2020 by the mercari R4D quantum team. Later, the paper was published in May 2021 in Physical Review A, a journal of American Physical Society (https://journals.aps.org/pra/abstract/10.1103/PhysRevA.103.052425). This work is in collaboration with QunaSys Inc.
Introduction
Quantum computer
There are certain types of computational problems of scale and complexity that cannot be solved by conventional computers in a realistic amount of time, but can be using quantum computers, such as physical simulation and prime factorization. Quantum computers therefore have important social and scientific application potential.
Stochastic differential equation
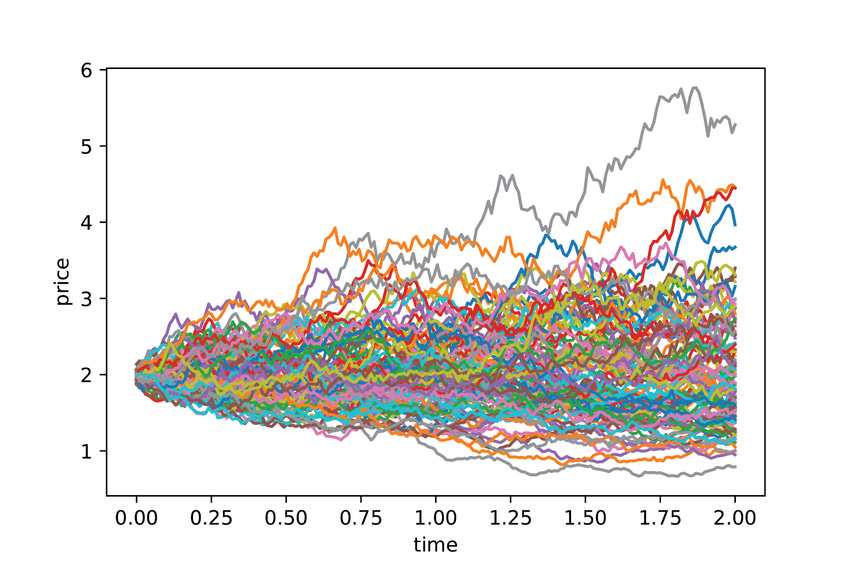
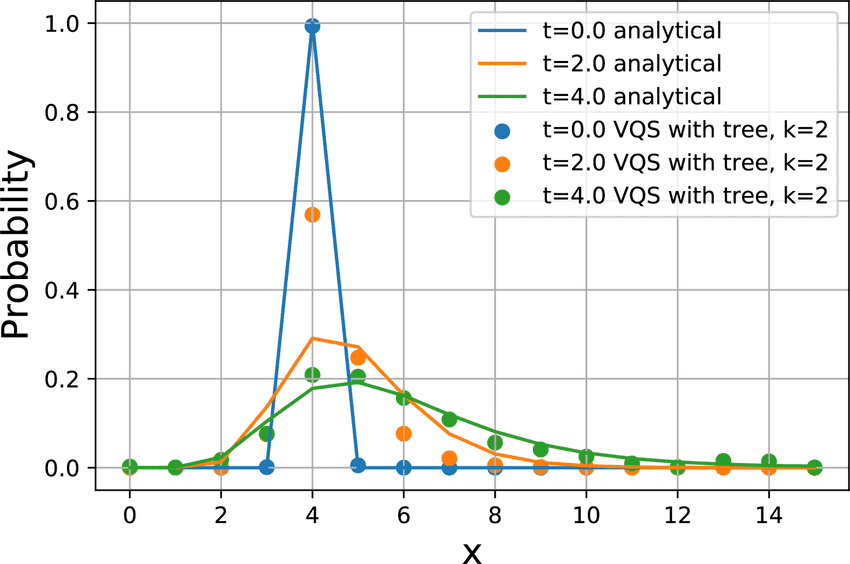
Predicting the future is an interesting challenge. But since it is generally impossible to predict what will happen in the future, we often use probabilities to model and compute. In particular, issues such as forecasting sales and demand, stock price fluctuations, and the spread of infectious diseases, are modeled on the probability of fluctuations over time. The “stochastic differential equation” discussed in this study is an equation that describes how probability changes over time. By solving stochastic differential equations, we can predict the uncertain future through probabilities. However, this can also lead to additional challenges, especially when there are many variables. Wondering whether quantum computers could be harnessed to solve stochastic differential equations at high speed was the starting point of this study.
Variational quantum simulation
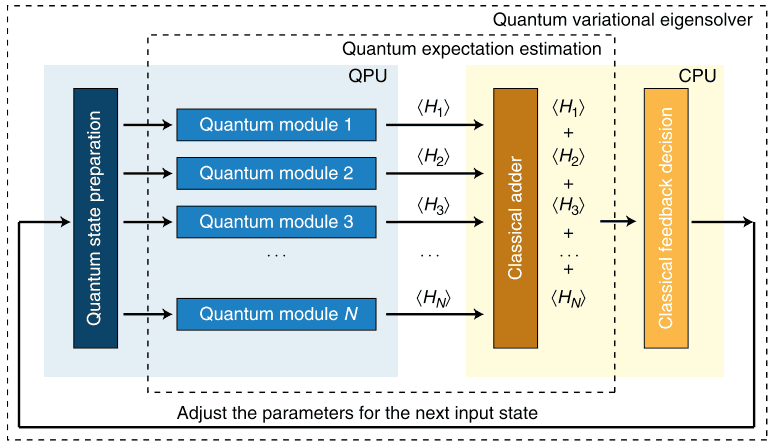
As of recent, hybrid quantum computing has been attracting attention among quantum algorithms. Hybrid quantum computing is an approach that leverages the strengths of both conventional and quantum computers through their combined use. Today’s quantum computers can perform large-scale matrix and vector calculations that conventional computers cannot handle. By contrast, current quantum computers find basic arithmetic operations difficult to handle, so here conventional computers are better suited. Hybrid quantum computing performs calculations that could not be done previously by conventional computers alone, by sharing these tasks. The “variational quantum simulation” covered in this study is such a hybrid quantum calculation, and although it is named “simulation,” it can be used to solve linear differential equations as well.
Contribution of this research
Method
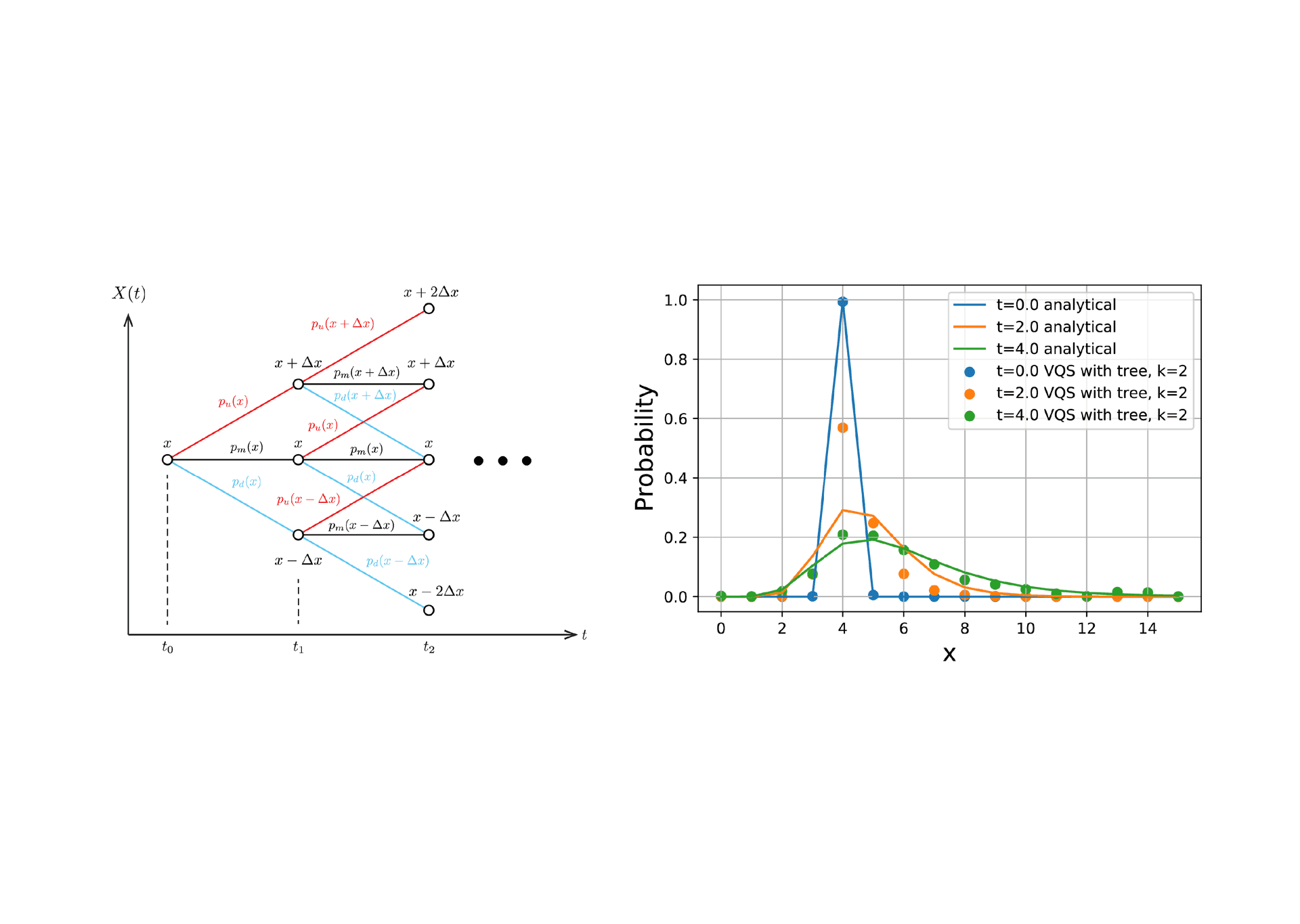
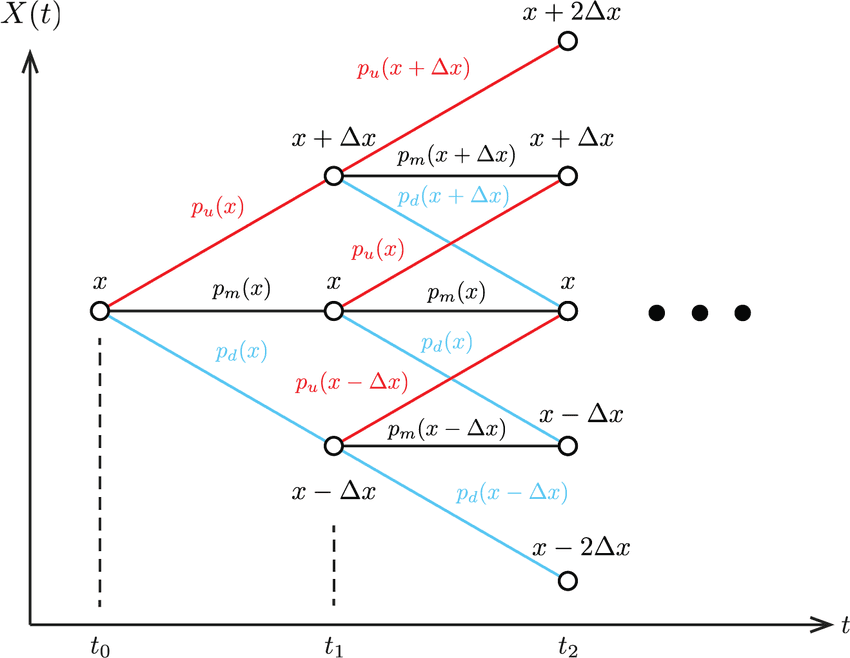
Variational quantum simulations can solve differential equations, but they cannot solve stochastic differential equations directly. We therefore proposed a method of deriving a differential equation for a probability distribution instead of a stochastic differential equation by modeling using a tree model[^1] and solving the obtained differential equation by applying variational quantum simulation. This made it possible to handle large-scale stochastic differential equations in variational quantum simulations. We applied this method using a simulator that reproduces the operation of a quantum computer, and confirmed that the method was indeed feasible.
Expected value calculation
Although the probability distribution dynamics can thus be obtained, in many cases it is favorable to find the expected value for some function that takes the probability distribution as an input, rather than the probability distribution itself. But with this method, conventional methods of calculating the expectation value cannot be used, since it relies on a new method to encode information (probability distribution) into a quantum state in order to simulate the probability distribution. We therefore proposed a method of efficiently calculating the expectation value of a function using the probability distribution represented by this new encoding method as the input when a function is given. We also showed that this method can reduce the size of the required quantum circuit compared to the conventional.
Future efforts
In this study, we present a method of simulating probability differential equations using quantum calculation and calculating expectation values using the simulation results. Moving forward, we will try to solve more complex problems by exploring specific applications of the proposed method and combining simulation and optimization.
[^1] An approximation method used in financial engineering that approximates a continuous stochastic process using discrete stochastic processes, during which the transition probability is determined so that the statistics match.
Kenji Kubo